Mössbauer Spectroscopy Group

Mössbauer spectroscopy is a versatile technique that can be used to provide information in many areas of science such as Physics, Chemistry, Biology and Metallurgy. It can give very precise information about the chemical, structural, magnetic and time-dependent properties of a material. Key to the success of the technique is the discovery of recoilless gamma ray emission and absorption, now referred to as the 'Mössbauer Effect', after its discoverer Rudolph Mössbauer, who first observed the effect in 1957 and received the Nobel Prize in Physics in 1961 for his work. 

This introduction to the theory and applications of Mössbauer spectroscopy is composed of four sections. First the theory behind the Mössbauer effect is explained. Next how the effect can be used to probe atoms within a system is shown. Then the principal factors of a Mössbauer spectrum are illustrated with spectra taken from research work. Finally a bibliography of books and web sites is given for further and more detailed information. 

The Mössbauer Effect

Nuclei in atoms undergo a variety of energy level transitions, often associated with the emission or absorption of a gamma ray. These energy levels are influenced by their surrounding environment, both electronic and magnetic, which can change or split these energy levels. These changes in the energy levels can provide information about the atom's local environment within a system and ought to be observed using resonance-fluorescence. There are, however, two major obstacles in obtaining this information: the 'hyperfine' interactions between the nucleus and its environment are extremely small, and the recoil of the nucleus as the gamma-ray is emitted or absorbed prevents resonance. 

In a free nucleus during emission or absorption of a gamma ray it recoils due to conservation of momentum, just like a gun recoils when firing a bullet, with a recoil energy E_R. This recoil is shown in Fig1. The emitted gamma ray has E_R less energy than the nuclear transition but to be resonantly absorbed it must be E_R greater than the transition energy due to the recoil of the absorbing nucleus. To achieve resonance the loss of the recoil energy must be overcome in some way.

As the atoms will be moving due to random thermal motion the gamma-ray energy has a spread of values E_D caused by the Doppler effect. This produces a gamma-ray energy profile as shown in Fig2. To produce a resonant signal the two energies need to overlap and this is shown in the red-shaded area. This area is shown exaggerated as in reality it is extremely small, a millionth or less of the gamma-rays are in this region, and impractical as a technique.

What Mössbauer discovered is that when the atoms are within a solid matrix the effective mass of the nucleus is very much greater. The recoiling mass is now effectively the mass of the whole system, making E_R and E_D very small. If the gamma-ray energy is small enough the recoil of the nucleus is too low to be transmitted as a phonon (vibration in the crystal lattice) and so the whole system recoils, making the recoil energy practically zero: a recoil-free event. In this situation, as shown in Fig3, if the emitting and absorbing nuclei are in a solid matrix the emitted and absorbed gamma-ray is the same energy: resonance!

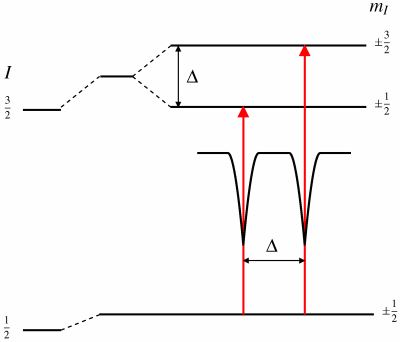
If emitting and absorbing nuclei are in identical, cubic environments then the transition energies are identical and this produces a spectrum as shown in Fig4: a single absorption line.

Now that we can achieve resonant emission and absorption can we use it to probe the tiny hyperfine interactions between an atom's nucleus and its environment? The limiting resolution now that recoil and doppler broadening have been eliminated is the natural linewidth of the excited nuclear state. This is related to the average lifetime of the excited state before it decays by emitting the gamma-ray. For the most common Mössbauer isotope, ⁵⁷Fe, this linewidth is 5x10^-9ev. Compared to the Mössbauer gamma-ray energy of 14.4keV this gives a resolution of 1 in 10¹², or the equivalent of a small speck of dust on the back of an elephant or one sheet of paper in the distance between the Sun and the Earth. This exceptional resolution is of the order necessary to detect the hyperfine interactions in the nucleus.

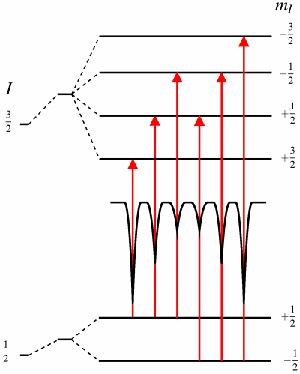
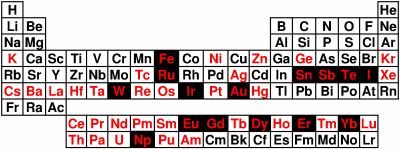
As resonance only occurs when the transition energy of the emitting and absorbing nucleus match exactly the effect is isotope specific. The relative number of recoil-free events (and hence the strength of the signal) is strongly dependent upon the gamma-ray energy and so the Mössbauer effect is only detected in isotopes with very low lying excited states. Similarly the resolution is dependent upon the lifetime of the excited state. These two factors limit the number of isotopes that can be used successfully for Mössbauer spectroscopy. The most used is ⁵⁷Fe, which has both a very low energy gamma-ray and long-lived excited state, matching both requirements well. Fig5 shows the isotopes in which the Mössbauer effect has been detected.

Armed with the Mössbauer effect and a suitable isotope how can we use these properties to investigate a system? This will be explained in Part 2.

 

So far we have seen one Mössbauer spectrum: a single line corresponding to the emitting and absorbing nuclei being in identical environments. As the environment of the nuclei in a system we want to study will almost certainly be different to our source the hyperfine interactions between the nucleus and the its environment will change the energy of the nuclear transition. To detect this we need to change the energy of our probing gamma-rays. This section will show how this is achieved and the three main ways in which the energy levels are changed and their effect on the spectrum.

Fundamentals of Mössbauer Spectroscopy

As shown previously the energy changes caused by the hyperfine interactions we will want to look at are very small, of the order of billionths of an electron volt. Such miniscule variations of the original gamma-ray are quite easy to achieve by the use of the doppler effect. In the same way that when an ambulance's siren is raised in pitch when it's moving towards you and lowered when moving away from you, our gamma-ray source can be moved towards and away from our absorber. This is most often achieved by oscillating a radioactive source with a velocity of a few mm/s and recording the spectrum in discrete velocity steps. Fractions of mm/s compared to the speed of light (3x10¹¹mm/s) gives the minute energy shifts necessary to observe the hyperfine interactions. For convenience the energy scale of a Mössbauer spectrum is thus quoted in terms of the source velocity, as shown in Fig1.

With an oscillating source we can now modulate the energy of the gamma-ray in very small increments. Where the modulated gamma-ray energy matches precisely the energy of a nuclear transition in the absorber the gamma-rays are resonantly absorbed and we see a peak. As we're seeing this in the transmitted gamma-rays the sample must be sufficiently thin to allow the gamma-rays to pass through, the relatively low energy gamma-rays are easily attenuated.

In Fig1 the absorption peak occurs at 0mm/s, where source and absorber are identical. The energy levels in the absorbing nuclei can be modified by their environment in three main ways: by the Isomer Shift, Quadrupole Splitting and Magnetic Splitting.

Isomer Shift

The isomer shift arises due to the non-zero volume of the nucleus and the electron charge density due to s-electrons within it. This leads to a monopole (Coulomb) interaction, altering the nuclear energy levels. Any difference in the s-electron environment between the source and absorber thus produces a shift in the resonance energy of the transition. This shifts the whole spectrum positively or negatively depending upon the s-electron density, and sets the centroid of the spectrum.

As the shift cannot be measured directly it is quoted relative to a known absorber. For example ⁵⁷Fe Mössbauer spectra will often be quoted relative to alpha-iron at room temperature.

The isomer shift is useful for determining valency states, ligand bonding states, electron shielding and the electron-drawing power of electronegative groups. For example, the electron configurations for Fe²⁺ and Fe³⁺ are (3d)⁶ and (3d)⁵ respectively. The ferrous ions have less s-electrons at the nucleus due to the greater screening of the d-electrons. Thus ferrous ions have larger positive isomer shifts than ferric ions.

Quadrupole Splitting

Nuclei in states with an angular momentum quantum number I>1/2 have a non-spherical charge distribution. This produces a nuclear quadrupole moment. In the presence of an asymmetrical electric field (produced by an asymmetric electronic charge distribution or ligand arrangement) this splits the nuclear energy levels. The charge distribution is characterised by a single quantity called the Electric Field Gradient (EFG).

In the case of an isotope with a I=3/2 excited state, such as ⁵⁷Fe or ¹¹⁹Sn, the excited state is split into two substates m_I=±1/2 and m_I=±3/2. This is shown in Fig2, giving a two line spectrum or 'doublet'.

The magnitude of splitting, Delta, is related to the nuclear quadrupole moment, Q, and the principle component of the EFG, V_zz, by the relation Delta=eQV_zz/2.

Magnetic Splitting

In the presence of a magnetic field the nuclear spin moment experiences a dipolar interaction with the magnetic field ie Zeeman splitting. There are many sources of magnetic fields that can be experienced by the nucleus. The total effective magnetic field at the nucleus, B_eff is given by:

B_eff = (B_contact + B_orbital + B_dipolar) + B_applied

the first three terms being due to the atom's own partially filled electron shells. B_contact is due to the spin on those electrons polarising the spin density at the nucleus, B_orbital is due to the orbital moment on those electrons, and B_dipolar is the dipolar field due to the spin of those electrons.

This magnetic field splits nuclear levels with a spin of I into (2I+1) substates. This is shown in Fig3 for ⁵⁷Fe. Transitions between the excited state and ground state can only occur where mI changes by 0 or 1. This gives six possible transitions for a 3/2 to 1/2 transition, giving a sextet as illustrated in Fig3, with the line spacing being proportional to B_eff.

The line positions are related to the splitting of the energy levels, but the line intensities are related to the angle between the Mössbauer gamma-ray and the nuclear spin moment. The outer, middle and inner line intensities are related by:

3 : (4sin²theta)/(1+cos²theta) : 1

meaning the outer and inner lines are always in the same proportion but the middle lines can vary in relative intensity between 0 and 4 depending upon the angle the nuclear spin moments make to the gamma-ray. In polycrystalline samples with no applied field this value averages to 2 (as in Fig3) but in single crystals or under applied fields the relative line intensities can give information about moment orientation and magnetic ordering.

These interactions, Isomer Shift, Quadrupole Splitting and Magnetic Splitting, alone or in combination are the primary characteristics of many Mössbauer spectra. The next section will show some recorded spectra which illustrate how measuring these hyperfine interactions can provide valuable information about a system.

 

This section shows how Mössbauer spectroscopy can be a useful analytical tool for studying a variety of systems and phenomena. The spectra have been taken from active research projects and chosen to visually represent the hyperfine interactions presented in Part 2 and how they can be interpreted.

Example Spectra

Tin dioxide assisted antimony oxidation

Antimony-containing tin dioxide is an important catalyst for selective oxidation of olefins. Of particular importance in studying these systems to is to know the relative concentrations of the antimony charge states (3+ and 5+) during the catalytic process.

Fig1 shows three ¹²¹Sb spectra taken at various stages during the catalytic process: 1) fresh Sb₂O₃, 2) Sb₂O₃ calcined at 1000C and 3) the calcined material after catalysis. Firstly the isotope-specificity of Mössbauer spectroscopy picks out only the antimony atoms from the Sn-Sb-O composite. Readily apparent from spectrum 1 is that practically all of the antimony is in a single state (the red component). Comparison with previous experiments shows that the isomer shift for this majority component matches that of Sb3+. The asymmetric shape is due to the quadrupole splitting in this isotope, which has 8 lines (it is a 7/2 to 5/2 transition).

After calcining the spectrum is now composed of two components of equal area. The second (green) component corresponds to the Sb5+ ion. The component areas give the relative proportion of each site within the compound, in this case 1:1 indicating either Sb₂O₄ or Sb₆O₁₃. After the catalysis in spectrum 3 we can see that the antimony is now all in the 3+ charge state again.

Tin spectra were also recorded, showing a single line spectrum of identical isomer shift during all parts of the process, indicating no change in the tin charge state.

In cases like this basic deductions can be made even without computer analysis: one can simply see one component appear and disappear and the differences in isomer shift are readily apparent. Unfortunately it isn't always quite this obvious!

Off-center tin atoms in PbSnTeSe

Off-center impurities are those which can be displaced from their regular positions in a crystal lattice. They can be considered as existing in an asymmetric double potential well. Such atoms can change their position as the temperature changes. Unfortunately there are often many other phenomena in such systems that can mask the off-centering effect.

Mössbauer spectroscopy provides a good tool for observing this effect. Firstly the movement of the off-center atom within the lattice will change the symmetry of the electric field it is in: hence changing the quadrupole splitting. Mössbauer spectroscopy is also isotope and site specific, meaning we can observe the off-center single component without any masking from other elements or effects.

A compound which was thought to exhibit off-centering is Pb_0.8Sn_0.2Te_0.8Se_0.2, with tin as an off-center atom. Spectra are shown in Fig2 from this sample at 200K and 20K. There are two components: one from an off-center site and one from a normal single-potential site. It can be seen in the highlighted region that the small green component develops from a single line to a (broad) doublet. The quadrupole splitting is increasing, indicating the electric field environment around these particular atoms is become more asymmetrical. This is consistent with an atom moving within an asymmetric potential well.

The other component shows no variation in quadrupole splitting. A series of spectra were taken in a temperature cycle and a hysteresis was observed in the values of quadrupole splitting. These results show that tin is an off-center atom in this compound and that there are two tin sites within it: one normal and one off-center.

Uranium/Iron multilayers

 

Magnetic multilayers are very important in today's technology, particularly in the areas of data storage and retrieval. A recent development is the use of actinides, such as uranium. Uranium in the right environment displays very large orbital magnetic moments, crucial to engineering systems with strong magnetic anisotropy and for magneto-optical applications. As part of this research sputtered Uranium/Iron multilayers have been produced and Mössbauer spectroscopy has been used to investigate the state of the iron within them.

As these samples are sputtered onto a thick substrate we cannot use conventional Mössbauer spectroscopy in Transmission Mode (TM) as the substrate would block the gamma-rays and we would receive no signal at all. There is a technique known as Conversion Electron Mössbauer Spectroscopy or CEMS which records the conversion electrons emitted by the resonantly excited nuclei in the absorber. In TM mode we record the absorption peaks as the gamma-rays are resonantly absorbed and so see dips, whilst in CEMS we record the electrons emitted from those excited nuclei and so see emission peaks. As the electrons are strongly attenuated by the sample as they pass through it most of the signal only comes from the uppermost 1000Angstroms.

Fig3 shows ⁵⁷Fe CEMS spectra from three Uranium/Iron multilayers of varying layer thicknesses. They are composed of three components: two sextets and one doublet. The hyperfine parameters of the two sextets correspond to alpha-iron, the red component being fully crystalline and the green component being from diffuse and poorly crystalline alpha-iron. The magnetic splitting shows that the iron in these two components is magnetically ordered.

The third component has an isomer shift and quadrupole splitting consistent with previous work on the UFe₂ intermetallic. This is paramagnetic at room temperature, as shown by the doublet. It is a doublet and not a sextet even though the intermetallic has a magnetic moment as the moment direction changes much faster in the paramagnetic state than the time it takes Mössbauer spectroscopy to record it and thus the experienced hyperfine field averages to zero.

As the iron layer thickness is increased to 43Angstroms the relative proportion of alpha-iron to UFe₂ increases and also the proportion of fully crystalline iron increases. As the iron layer is increased further to 180Angstroms this proportion becomes even greater. We can deduce from this that the thicker the iron layer the greater the proportion of crystalline iron, but more detailed analysis of the component areas compared to the layer thickness shows that the absolute thicknesses of the poorly crystalline iron and UFe₂ stay roughly constant.

Mössbauer spectroscopy has easily shown the existence of the three different iron sites within the sample and how their proportion has varied with layer thickness.

Superspin glass transition in Al₄₉Fe₃₀Cu₂₁

The magnetic properties of granular alloys and heterogeneous nanostructures built by ferromagnetic and non-magnetic components attract much attention due both to the fundamental interest of their rich phenomenology and to their potential applications, for instance in magnetoresistive devices and magnetic recording. Of particular interest are superspin glasses but their study is made difficult by the different possible sources for non-equilibrium magnetic behaviour and the mixtures of particle phases within the samples.

Mössbauer spectroscopy, as seen in the previous examples, is very good at distinguishing particular sites or phases within a sample. And as seen in the previous example can show the difference between magnetically ordered and paramagnetic sites. As the superspin glass phase reaches its freezing temperature the atoms become magnetically ordered and this will show up in the spectra as a sextet appearing.

A series of ⁵⁷Fe spectra were recorded from a ball-milled sample of Al₄₉Fe₃₀Cu₂₁ with decreasing temperature, shown in Fig4. At 40K, above the freezing temperature, there are two components of unequal proportion, both doublets. As the temperature is reduced the smaller component starts to spread outwards into a magnetic sextet. The peaks are broad and diffuse due to there being a distribution of grain sizes within the sample and hence a distribution of magnetic hyperfine fields. Plotting the recorded hyperfine field against temperature can then give the superspin glass transition temperature for this compound.

Mössbauer spectroscopy showed quite readily the onset of the superspin glass 'freezing' and the proportion of the magnetic particles and their surrounding non-magnetic matrix. Analysis of the hyperfine field distribution also proved consistent with that expected for a superspin glass.This section shows how Mössbauer spectroscopy can be a useful analytical tool for studying a variety of systems and phenomena. The spectra have been taken from active research projects and chosen to visually represent the hyperfine interactions presented in Part 2 and how they can be interpreted.

This introduction has covered some of the basics of Mössbauer spectroscopy but there are still numerous further theoretical and practical aspects to the discipline. For those who are interested in learning more about the physics or applications of the Mössbauer effect we have provided a collection of useful web sites and literature.

Books

• Mössbauer Spectroscopy and its Applications, T E Cranshaw, B W Dale, G O Longworth and C E Johnson, (Cambridge Univ. Press: Cambridge) 1985
• Mössbauer Spectroscopy, D P E Dickson and F J Berry, (Cambridge Univ. Press: Cambridge) 1986
• The Mössbauer Effect, H Frauenfelder, (Benjamin: New York) 1962
  Principles of Mössbauer Spectroscopy, T C Gibb, (Chapman and Hall: London) 1977
• Mössbauer Spectroscopy, N N Greenwood and T C Gibb, (Chapman and Hall: London) 1971
• Chemical Applications of Mössbauer Spectroscopy, V I Goldanskii and R H Herber ed., (Academic Press Inc: London) 1968
• Mössbauer Spectroscopy Applied to Inorganic Chemistry Vols. 1-3, G J Long, ed., (Plenum: New York) 1984-1989
• Mössbauer Spectroscopy Applied to Magnetism and Materials Science Vol. 1, G J Long and F Grandjean, eds., (Plenum: New York) 1993  

For useful websites, see the Related Links below.