Ab initio SCF-MO study of the Staudinger reaction between a phosphane and an Azide to form a Phosphazene.

Mateo Alajarin^a, Carlota Conesa^a,b and Henry S. Rzepa*^b

Summary

The lowest energy pathway for Staudinger reaction between a phosphane and an azide is predicted at the RHF and DFT ab initio SCF-MO level to proceed via a s-cis intermdiate 7, followed by cyclisation and elimination of N₂ to form a phosphazene. When suitable stabilising substituents are present, 7 can instead isomerise to the isolable s-trans intermediate 9. Natural bond orbital perturbation theory analysis has been employed to identify the factors influencing the relative stability of the s-cis phosphazide and the s-trans isomers.

 

The structure of the phosphazide intermediate 3 was subject of some controversy^1d,2 until X-ray structural data became available^1d,3. Although they are not usually stable, some phosphazides have been isolated⁴. Most of these stable phosphazides present distinctive characteristics such as a) the presence of electron withdrawing substituents on the azido end and/or electron donating substituents on the phosphorus atom, b) the presence of very bulky substituents (R and/or R'), and c) the presence of acidic hydrogen atoms capable of forming intramolecular hydrogen bonds with the N atoms of the PN₃ unit.

Herein, we present the results of ab initio Hartree-Fock and Density Functional Theory calculations which provide insight into the mechanism of this reaction, and which can offer suitable explanations for some of the experimental facts.

Computational Procedure.

Approximate geometries were initially optimized at the PM3 level using the MOPAC V6.0 program⁵ implemented on CAChe workstations. The transition structures were located by using eigenvector following routine (TS). This procedure was followed by ab initio calculations performed using the GAUSSIAN94 and 98 program systems⁶, transition states being located by using the Berny algorithm⁷ or the synchronous transit-guided quasi-Newton (STQN) methods implemented by Schlegel⁸. A Natural Bond Orbital (NBO) analysis⁹ was invoked using the population keyword in GAUSSIAN94/98. Molecular co-ordinates in the form of pdb files for located stationary points are integrated into this article, together with animations of all important imaginary modes showing the form of the eigenvectors.

Results and Discussion.

Factors influencing the Relative Stability of 7 and 9.

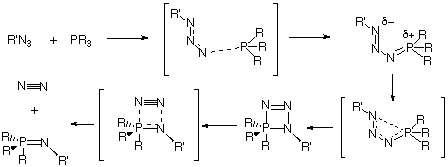
Our first aim was to reconcile why almost all the reported X-ray structural data of phosphazides 3 revealed a species with a central N-N bond with the s-trans configuration 9 (Scheme 2), whereas the subsequent extrusion of nitrogen and the formation of an N-P bond requires a s-cis configuration 7.

Our results predict the unsubstituted s-cis isomer 7 (R=R'=H) to in fact be more stable¹⁰ than the s-trans isomer 9, by 6.6 kcal/mol at the HF level and 9.4 and 8.7 kcal/mol at the B3LYP/6-31G* and 6-311G** levels respectively (Table 1). A simple rationalisation is in terms of favourable electrostatic interactions between the partially positive phosphorus atom (Mulliken charge +0.54/B3LYP/6-31G*) and the partially negatively charged nitrogen atom (-0.37/B3LYP/6-31G*) in the s-cis isomer 7. The geometry of the s-trans isomer also shows a significant double bond character for the N-P bond. This bond distance is longer for the s-cis isomer, which also shows a shortening of the central N-N bond (Figure 1).

A study of the potential energy surface for the formation of 3 revealed that not only was the s-cis isomer 7 route the most stable but also corresponded to the pathway with the lowest energy barrier. The transition state 8 for N-P bond formation has an energy barrier of 61.8 kcal/mol, which is 25.9 kcal/mol larger than the alternative 6 at the RHF level, whilst 8 could not could even be located at the DFT level. A further study of the potential energy surface allowed us to locate another transition structure 10, corresponding to the isomerization of the phosphazide molecule by rotation of the central N-N bond. The location of this transition structure meant that the s-trans isomer could be formed from the s-cis isomer by isomerization,with a readily accessible energy barrier (Table 1) of 20.8 kcal/mol (HF) or 16.46 kcal/mol (B3LYP).

Our results for R=R'=H did not explain why only the s-trans configuration is found for those exceptionally stablised phosphazides which have been isolated. To identify why such stabilization takes a greater effect on the s-trans isomer than on the s-cis, we calculated systems with either a cyano substituent on the nitrogen atom (R'=CN, R=H) or a p electron-donating substituents on the phosphorus atom (R'=H, R=OMe). In the first case, the difference between the energy of the s-cis and s-trans isomers was reduced from 9.4 (R=R'=H) to 5.9 kcal/mol at RHF level. In the second case (R'=H, R=OMe) the s-trans isomer was indeed found to be very slightly more stable than the s-cis isomer at the RHF/6-31G* and B3LYP/6-311G** levels (Table 1). The energy barrier for the formation of the phosphazide for R'=H, R=OMe was still lower for the s-cis isomer. We suggest therefore that the formation of stabilised s-trans isomers takes place via the formation and subsequent isomerisation of the s-cis phosphazide by rotation of the central N-N bond.

In order to get a deeper insight into the factors that control the relative stability of the s-cis and s-trans isomers, we made use of the Natural Bond Orbital (NBO) analysis, a method which has been previously employed in the study of the cis-effect in 1,2-difluoroethene and other organic molecules¹¹. We note firstly that for the case of R=R'=H, the NBO (RHF/6-31G* level) shows a one-centre p lone pair n_p(N_a) on the N atom connected to the P, rather than a two-centre p bond between the N_a and P atoms. The most significant difference between the two isomers is that the term corresponding to the interaction n_p(N_a) to p*(N_b=N_g)  is 58.8 kcal/mol for the s-trans isomer and 95.5 kcal /mol for the s-cis . The difference is due to the differences in energy between both orbitals ( 0.47 Hartree for s-cis and 0.50 Hartree for s-trans)  and in the Fock matrix element ( 0.195 Hartree for s-cis and 0.161 Hartree for s-trans). In addition, the antiperiplanar contributions also favour the s-cis isomer. Thus the antiperiplanar interaction  n_s( N_b) to s*( N_a-P ) is large for the s-cis whereas it is insignificant for synperiplanar s-trans interaction (16.7 kcal/mol vs 0.7 kcal/mol). The interaction n_s(N_a) to s*(N_b=N_g) is analogous (8.2 kcal/mol vs 0.7 kcal/mol). For the substituted system (R=OMe, R'=H) the NBO shows in contrast a p orbital between N_a-P rather than an n lone pair on N_a, although the contribution to this orbital is mainly from the N (93%). In this case, the term for the interaction p(N_a=P) to p* (N_b=N_g)  is 50.2 kcal/mol for the s-trans isomer and 41.75 kcal/mol for the s-cis. The Fock matrix element is the same for both isomers and the difference is due to both orbitals being closer in energy for the s-trans isomer (0.67 Hartree vs. 0.57 Hartree).  Although the antiperiplanar contributions are still in favour of the s-cis isomer, e.g. n_s( N_b) to s*( N_a-P ) is 13.70 kcal/mol for s-cis and 0.5 kcal/mol for s-trans and similarly n_s(N_a) to s*(N_b=N_g) is 9.2 kcal/mol for s-cis vs 1.0 kcal/mol for s-trans, they do not seem to be enough to make the s-cis isomer more stable.

Potential surface for the subsequent reaction of 7.

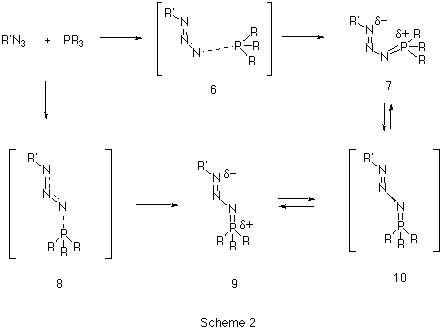
The second step of the Staudinger reaction takes place when the s-cis-phosphazide undergoes cyclization to form the four-membered cyclic intermediate 13 (Scheme 3). Such cyclization would be expected¹¹ to take place via a nucleophilic apical attack of the terminal nitrogen atom at one of the faces of the tetrahedral phosphorus. This mechanism would produce cycle 12 with the sp³ nitrogen atom in an apical position. Given the known¹² apicophobic character of the NH₂ moiety, this species would evolve via pseudorotation^12,13, to the a priori more stable isomer 13, in which the sp² nitrogen atom is in an apical position because of the increase in apicophilicity of substituents in pentavalent phosphorus on increasing the electronegative character. However, the cyclization transition state 11 (Figure 2), was found to link Z-phosphazide 7 with the cyclic isomer 13 without the intermediacy of 12. The vibrational analysis of transition structure 11 shows a rotation of the N-P bond simultaneous to the approach of the nitrogen and phosphorus atoms. The energy of 11, at least with R=R'=H is in fact lower than for 10, which explains why the s-cis-phosphazides are not usually isolated. Subsequently, the extrusion of a nitrogen molecule from the cyclic intermediate can take place by fragmentation of the P-N bond in the apical position (transition state 14) without the need for a pseudo-rotation process.Again, the energy of 14 is lower than than 10, confirming that a low energy route does exist for nitrogen extrusion compared to isomerisation (Figure 3).
 

Conclusions.

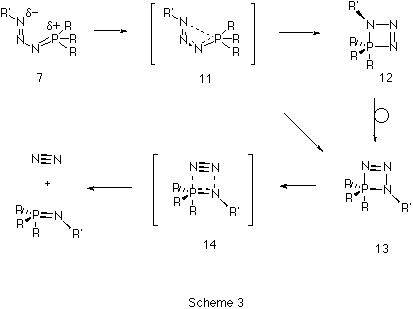
At the ab initio RHF and B3LYP levels of theory, we predict that the Staudinger reaction consists of a sequence of reactions shown diagrammatically in Figure 3. Nucleophilic attack of the phosphane on the terminal nitrogen of an azide forms the corresponding s-cis-phosphazide 7, which in turn can either isomerize to the s-trans isomer 9, which would only be stable and isolable if appropriate substituents are present, or readily cyclize to form the cyclic intermediate 13. Elimination of a nitrogen molecule would form the corresponding phosphazene 4. Results on larger substituted systems of synthetic interest will be reported in a subsequent article.

References

[1] (a) H. Staudinger, J. Meyer, Helv. Chim. Acta 1919, 2, 635; b) Y. G. Gololobov, L. F. Kasukhin, Tetrahedron 1992, 48, 1353; c) Y. G. Gololobov, I. N. Zhmurova, L. F. Kasukhin, ibid. 1981, 37, 437; d) A. W. Johnson, Ylides and Imines of Phosphorus, Wiley, New York, 1993, p. 403.
[2] J.S. Thayer, R.West, Inorg Chem. 1964, 3, 406; J.E. Leffler, U. Honsberg, Y, Tsuno, I. Forsblad, J. Org. Chem., 1961, 26, 4810.
[3] G.L. Hillhouse, G.V. Goeden, B. L. Haymore, Inorg. Chem. 1982, 21, 2064.
[4] (a) J. R. Goerlich, M. Farkens, A. Fischer, P. G. Jones, R. Schmutzler, Z. Anorg. Allg. Chem. 1994, 620, 707; A. N. Chernega, M. Y. Antipin, Y. T. Struchkov, I. E. Boldeskul, M. P. Ponomarchuk, L. F. Kasukhin, V. P. Kukhar, Zh. Obshch. Khim. 1984, 54, 1979; A. N. Chernega, M. Y. Antipin, Y. T. Struchkov, M. P. Ponomarchuk, L. F. Kasukhin, V. P. Kukhar, ibid. 1989, 59, 1256; A. A. Tolmachev, A. N. Kostyuk, E. S. Kozlov, A. P. Polishchuk, A. N. Chernega, ibid. 1992, 62, 2675; G. L. Hillhouse, G. V. Goeden, B. L. Haymore, Inorg. Chem. 1982, 21, 2064; C. K. Lowe-Ma, R. A. Nissan, W. S. Wilson, J. Org. Chem. 1990, 55, 3755; R. W. Saalfrank, E. Ackermann, M. Fisher, U. Wirth, H. Zimmerman, Chem. Ber. 1990, 123, 115; J. Kovacs, I Pinter, M. Kajtar-Peredy, L Somsak, Tetrahedron, 1997, 53, 1541; M. Hirsch-Kuchma, T. Nicholson, A. Davison, W. M. Davis, A. G. Jones, J. Chem. Soc., Dalton Trans., 1997, 3185; b) P. Molina, C. López-Leonardo, J. Llamas-Botía, C. Foces-Foces, C. Fernández-Castaño, Tetrahedron 1996, 52, 9629; c) C. G. Chidester, J. Szmuszkovicz, D. J. Duchamp, L. G. Laurian, J. P. Freeman, Acta Crystallogr. Sect. C 1988, 44, 1080;
[5] J.J.P.Stewart, MOPAC, Quantum Chemistry Program Exchange, University of Indiana, Bloomington, USA, Program 455.
[6] Gaussian program systems available from Gaussian Inc., 4415 Fifth Avenue, Pittsburgh, PA, USA.
[7] H.B. Schlegel, J.Comp.Chem., 1982, 3, 214.
[8] C. Peng, H.B. Schlegel, Israel J. Chem., 1993, 33, 449
[9] A.E. Reed, L.A. Curtis, F. Weinhold, Chem. Rev., 1988, 88, 899
[10] An early and to the best of our knowledge the only previous quantum mechanics study^4b on phosphazides, reported the Z configuration of PH₃N₃CH₃ to be 1.6 kcal mol^-1 more stable than the E isomer at HF/6-31G** level.
[11] P.vR. Scheleyer, M. Kaupp, F. Hampel, M. Bremer, K. Mislow, J. Am. Chem. Soc. 1992, 114, 6791. T. Yamamoto and S. Tomodo, Chem. Let., 1997, 1069-1070.
[12] P. Gillespie, F. Ramirez, I. Ugi, D. Marquarding, Angew. Chem. Int. Ed.Engl. 1973, 12, 91.
[13] D. G. Gilheany on The Chemistry of Organophosphorus compounds, The chemistry of functional groups series, editor S. Patai, Vol3, Chapter 1. Wiley & Sons, 1994.
 

Figure 1. B3LYP/6-311G** geometries for Ground states 9 and 7, and Transition states 6,8 and 10.

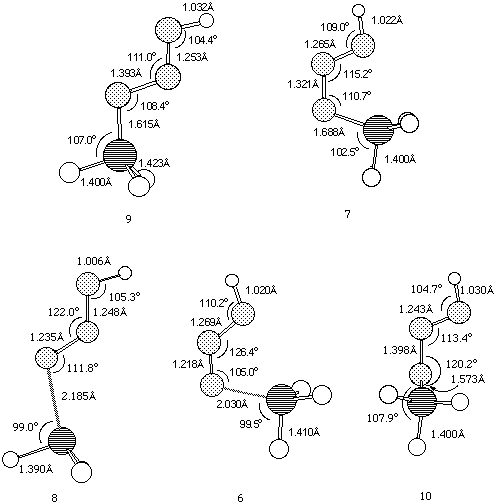
Figure 2. B3LYP/6-311G** geometries for structures 11-14

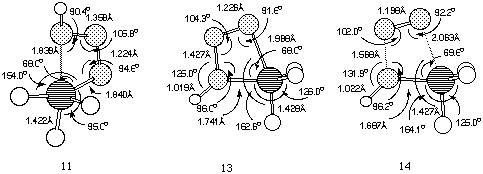
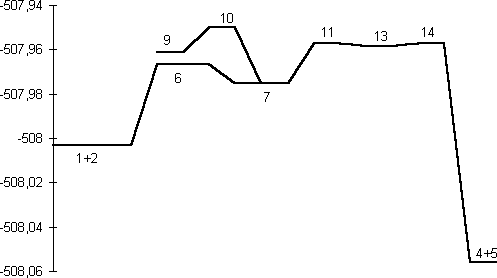
Table 1. Absolute and Relative (to 1+2) Energies and imaginary normal modes for the stationary point structures in the transformation 1+2 to 4+5 (Figure 3).

	RHF/6-31G*		B3LYP/6-31G*		B3LYP/6-311G**
	Energy, Hartree (Energy relative to 1+2, kcal/mol)	n, cm-1	Energy, Hartree (Energy relative to 1+2, kcal/mol)	n, cm-1	Energy, Hartree (Energy relative to 1+2, kcal/mol)	n, cm-1
R=R'=H
1	-342.44795		-343.14027		-343.17284
2	-163.83869		-164.78228		-164.83053
6	-506.22902 (36.17)	-499.4	-507.88812 (21.61)	-325.2	-507.96675 (22.98)	-339.2
7	-506.26216 (15.37)		-507.89731 (15.83)		-507.97511 (17.73)
8	-506.18812 (61.84)	-573.8
9	-506.25172 (21.92)		-507.8818 (25.50)		-507.96130 (26.40)
10	-506.24131 (26.70)	-176.5	-507.87110 (32.29)	-200.5	-507.94970 (33.68)	-211.4
11	-506.23611 (31.78)	-350.4	-507.88096 (27.1)	-228.8	-507.95697 (29.12)	-251.2
13	-506.24157 (28.29)		-507.88159 (25.70)		-507.95829 (28.29)
14	-506.23536 (32.19)	-663.2			-507.95704 (29.07)	-542.0
4	-397.42731		-398.44640		-398.49981
R=OMe, R'=H
6	-847.967545		-851.50187		-851.67384
7	-848.02835		-851.56220		-851.73372
8	-847.92777
9	-848.03012		-851.56164		-851.73393
10	-848.02083		-851.55290		-851.72518
R=H, R'=CN
7	-597.98427		-600.13067		-600.22866
9	-597.97486		-600.11701		-600.21617

How to view the Hyperactive Molecules contained in the Table

To measure bond length or angles, proceed as follows:

• Using Chem3D plugin, select an atom by mouse clicking on it. To measure a distance, move the cursor to the second atom, and the distance will be displayed on the screen. To measure an angle, select the first atom, and then by holding the shift key down, the second. Move the cursor to the third atom to display the angle on the screen.
• Using Chime 2.0. From the pull down menu that appears when the mouse button is held down over the molecule (Mac) or the right hand mouse button is selected (Windows), go to Select/Mouse Click Action/distance or angle. Release the menu and click at the position of two (three) atoms. The value of the bond length or angle is displayed in the information box at the bottom of the browser.

Animations and Saving coordinates